旋转数组相关
旋转数组(字符串)
算法中有关旋转数组或旋转字符串类算法汇总,思想汇总
旋转数组
题目:给定一个数组,将数组中的元素向右移动k个位置,其中k是非负数。 力扣题目189:旋转数组
示例1:

示例2:

Tips:算法至少有三种不同的方法求解,尝试使用空间复杂度为O(1)的原地算法。
方法1:暴力法求解(大循环嵌套小循环)
//暴力法旋转
//执行用时:233 ms, 在所有 Java 提交中击败了29.45%的用户
//内存消耗:39.1 MB, 在所有 Java 提交中击败了72.73%的用户
//取模优化后:
//执行用时:234 ms, 在所有 Java 提交中击败了28.15%的用户
//内存消耗:38.9 MB, 在所有 Java 提交中击败了89.28%的用户
public int[] moveRightK(int[] nums, int k){
//循环嵌套时,内部循环将数组右移一位,
//外层循环k次,就完成了数组移动k个位置
if(nums.length == 0 || k == 0) return nums;
//可以用k对数组长度取模,减少不必要的循环次数
int count = k % nums.length; //真正的移动次数
for(int i = 0; i < count; i++){
//记录最后一个位置的数值,
//最后一个数字,放置在起点,完成一次移动
int temp = nums[nums.length-1];
for(int j = nums.length-1; j > 0; j--){
nums[j] = nums[j-1];
}
nums[0] = temp;
}
return nums;
}方法2:波浪式旋转 法(记录总移动次数)
//波浪式旋转(固定总移动次数,多次连续旋转)
//执行用时:1 ms, 在所有 Java 提交中击败了56.10%的用户
//内存消耗:39.1 MB, 在所有 Java 提交中击败了74.65%的用户
public int[] moveRightK(int[] nums, int k){
if(nums.length == 0 || k == 0) return nums;
//循环进行连续旋转,每次连续旋转(移动)至回到原点为止,
//总旋转次数等于数组长度
int count = 0; //记录总的移动次数
for(int i = 0; i < nums.length; i++){
int cur = i; //连续旋转过程中不断变化的位置
int pre = nums[i]; //记录上一位置的数值
//先进行旋转再判断,因此使用do while
do{
cur = (cur+k) % nums.length;
int temp = nums[cur];
nums[cur] = pre;
pre = temp;
count++;
}while(cur != i);
if(count >= nums.length) break; //移动次数到了就退出
}
return nums;
}方法3:额外数组法
//额外数组使用
//执行用时:1 ms, 在所有 Java 提交中击败了56.10%的用户
//内存消耗:39.1 MB, 在所有 Java 提交中击败了71.96%的用户
//优化后提交:模计算很耗性能,两次取模运算进行合并
//执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
//内存消耗:38.9 MB, 在所有 Java 提交中击败了85.94%的用户
public int[] moveRightK(int[] nums, int k){
//因为要对数组本身进行修改,直接复制出一个相同数组作为参照
if(nums.length == 0 || k == 0) return nums;
int[] newArr = nums.clone();
//根据复制出来的数组的值,直接在原数组中进行相应位置的覆盖即可
//int count = k % nums.length;//真实移动的长度(可优化)
for(int i = 0; i < nums.length; i++){
int newIndex = (i+k) % nums.length;//总和一次取模
nums[newIndex] = newArr[i];
}
return nums;
}方法4:耍杂技法(三次反转,原地算法,空间O(1))
//耍杂技(最帅、最高端、最效率的方法)
//执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
//内存消耗:39.3 MB, 在所有 Java 提交中击败了47.26%的用户
public int[] moveRightK(int[] nums, int k){
if(nums.length == 0 || k == 0) return nums;
//数组向右移动k次,因为是循环移动的,等价于:
//先总体反转,再前k个数字反转,后n-k个数字反转
//具体为什么,有时间再聊了
k = k % nums.length; //保证k是一个小于数组长度的值
reverseArr(nums,0,nums.length-1);
reverseArr(nums,0,k-1);
reverseArr(nums,k,nums.length-1);
return nums;
}
//进行数组的反转(制定起始位置的)
public int[] reverseArr(int[] nums, int start, int end){
//数组反转,使用双指针进行交换
while(start < end){
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
return nums;
}寻找旋转排序数组中的最小值
假设按照升序排序的数组在预先未知的某个点上进行了旋转。例如,数组[0,1,2,4,5,6,7]可能变成[4,5,6,7,0,1,2],请找出数组中的最小元素。
示例1:

示例2:

示例3:

Tips:寻找数组内部最小值,内部元素进行比较判断,使用二分法。
(元素不重复判断比较容易)
先判断整体l-r是否有序,有序说明左侧端点为最小,返回
以左侧端点为准方法:满足l < r 时,取中间位置mid的值,与左侧端点值进行比较
- 如果大于等于左侧端点,表示左侧部分有序,右侧部分无序,只考虑左侧部分
- 因为mid=(l+r)/2,即mid有可能和左侧位置重合,此时要去右侧寻找(左侧已经判断mid)
- 如果小于左侧端点,表示左侧无序,则最小值一定在左侧,只考虑左侧即可
- 最后当l=r时,如果到了这一步,说明当前值为最小值了
以右侧端点为准方法:同样在满足l<r时,取中间位置mid的值,与右侧端点值进行比较
- 如果小于右侧端点,说明右侧为有序,此时只能说明 l-mid 是无序的,因此要带着(mid值)
- 有可能mid点正好落在最小值上,如果r=mid-1,则失去了最小值,
- 这种情况可以在优化时提前判断mid是否为最小值来避免
- 如果大于右端点,说明右侧无序,且mid肯定不是最小,因此l=mid+1
- 最后当l=r时,到了这一步,说明当前就是最小值
//寻找旋转数组中的最小值(数组元素于不重复)
//以左端点为标准
//如果整体有序,则左端点为最小值,返回
//如果左边部分有序,说明最小值在右边
//如果左边部分无序,说明在左边
//执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
//内存消耗:37.7 MB, 在所有 Java 提交中击败了90.18%的用户
public int findMin(int[] nums) {
int l = 0, r = nums.length-1;
//不加l=r的情况,作为最后一种,直接输出l的值
while(l < r){
if(nums[l] < nums[r]) return nums[l]; //整体有序,返回左端点值
int mid = (l+r) / 2;
//当前值下降,返回当前值
if(mid > 0 && nums[mid] < nums[mid-1]) return nums[mid];
if(mid < nums.length-1 && nums[mid] > nums[mid+1]) return nums[mid+1];
if(nums[mid] >= nums[l]) l = mid+1; //左侧有序,在右边 ,有可能mid=l,但是不会有mid=r
else r = mid-1; //右侧无序,在左边
}
return nums[l];
}
//从右侧开始判断
//如果中值小于右端点,右侧有序,则最小值在左侧,此时包括中值(即中值也可能是最小值)r=mid,
//(可添加判断mid是否最小值消去)
//如果中值大于右端点,则最小值在右侧,且中值不可能是最小l=mid+1
//执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
//内存消耗:37.9 MB, 在所有 Java 提交中击败了76.68%的用户
public int findMin2(int[] nums) {
int l = 0, r = nums.length-1;
while(l < r){
if(nums[l] < nums[r]) return nums[l]; //整体有序,左端点即为最小
int mid = (l+r) / 2;
//提前判断,减少搜索次数
if(mid > 0 && nums[mid-1] > nums[mid]) return nums[mid];
if(mid < nums.length-1 && nums[mid] > nums[mid+1]) return nums[mid+1];
if(nums[mid] > nums[r]) l = mid+1;
else r = mid-1;
}
return nums[l];
}寻找旋转排序数组中的最小值Ⅱ(数组中数可重复)
题目:假设按照升序排序的数组在预先未知的某个点上进行了旋转。如数组[0,1,2,4,5,6,7]可能变成[4,5,6,7,0,1,2],请找出其中最小的元素。(注意:数组中可能存在重复的元素)
示例1:

示例2:

Tips:数组中元素可以重复,则当mid与端点值相等时,不能判断当前段内元素是否有序,可能先降后增
public int findMin(int[] nums) {
//寻找数组中的最小值(元素可重复)
//执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
//内存消耗:38.3 MB, 在所有 Java 提交中击败了78.46%的用户
int l = 0, r = nums.length-1;
while(l < r){
if(nums[l] < nums[r]) return nums[l];
int m = (l+r) / 2;
if(m > 0 && nums[m-1] > nums[m]) return nums[m];
if(m < nums.length-1 && nums[m] > nums[m+1]) return nums[m+1];
if(nums[m] > nums[l]) l = m+1;
else if(nums[m] < nums[l]) r = m-1;
else l++;
}
return nums[l];
}搜索旋转数组(在数组中搜索目标数)
题目:给你一个整数数组
nums,和一个整数target,该整数数组原本是按照升序排列,但输入时在某一个点上进行了数组的旋转。如数组[0,1,2,3,4,5,6,7]可能变成了[4,5,6,7,0,1,2,3]。问题:请你在数组中搜索target,蜀国数组中存在这个目标值,则返回它的索引,否则返回-1。
示例1:

示例2:

示例3:

Tips:使用二分法思想查找数
- 因为是有序数组旋转而来,那么使用二分时,一定有一部分有序
- 如果左边有序,且目标值在左边范围内,则考虑左边部分,
- 否则考虑右边部分
- 如果左边无序(右边有序),且目标值在右边范围内,则考虑右边部分,
- 否则考虑左边部分
- (根据两边有序的那一部分进行判断,因为有序的部分只需要比较就可以判断出目标值是否在其中,若不在则去另外的部分查找)
public int search (int[] A, int target) {
int l = 0, r = A.length-1;
while(l <= r){
int mid = (l+r) / 2;
if(A[mid] == target) return mid;
if(A[l] <= A[mid]){
//左边有序
if(target >= A[l] && target < A[mid]){
r = mid-1;
}else l = mid+1;
}else{
//右边有序
if(target > A[mid] && target <= A[r]){
l = mid+1;
}else r = mid-1;
}
}
return -1;
}搜索旋转数组2(在旋转后的数组中搜索可重复的目标)
题目:给定一个排序后的数组,包含n个整数,但这个数组已经被旋转过很多次了,次数不详。请编写代码找出数组中的某个元素,假设数组元素是按照升序排列的。若有多个相同元素,返回索引值最小的。
力扣81:搜索旋转排序数组Ⅱ 力扣1825:面试题10.03.搜索旋转数组
示例1:

示例2:

Tips:和搜索旋转数组1不同的地方是当前问题中数字可重复,在判断左右是否有序时充分考虑中值与端点值相等时的情况。
解题思路:
- 此题目添加了数组中数字可以重复,且目标值重复是取下标最小的(这个怎么找呢?)
- 数组中允许重复数字时,判断部分是否有序的标准就发生了变化,好像就不能那么用了,即中值与端点值相等时,不能判断是否为有序的,要单独考虑
- 思路步骤:只考虑左侧部分的所有情况,
- 如果中值等于目标值,则判断前一位是否相等,不相等时说明当前索引为最小,否则,
- 中值明确大于左端点值时,左侧明确有序,可判断目标值是否在该有序段内,
- 在左侧则只考虑左侧
- 否则一定在右侧
- 中值明确小于左端点值时,左侧明确无序,则右侧一定有序,判断目标值是否在右侧段
- 在右侧则只考虑右侧
- 否则一定在左侧
- 相等,不知道是否有序,移动端点后判断,即左端点+1,重新获取中值进行判断
public int search(int[] arr, int target) {
//二分法在旋转的有序数组中搜索目标数
//执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
//内存消耗:39.6 MB, 在所有 Java 提交中击败了65.54%的用户
if(arr.length == 0) return -1;
if(arr[0] == target) return 0;
int l = 0, r = arr.length-1;
while(l <= r){
int mid = (l + r) / 2;
//中值就是目标值是,查看前一位是否相等,不相等时返回当前索引为最小
if(arr[mid] == target){
while(mid > 0 && arr[mid-1] == target) mid--;
return mid;
}
if(arr[l] < arr[mid]){
//中值明确大于左端点时,左边是有序的
if(target >= arr[l] && target < arr[mid]) r = mid-1;
else l = mid+1;
}
else if(arr[l] > arr[mid]){
//中值明确小于左端点时,左边是无序的,则右侧一定有序了
if(target > arr[mid] && target <= arr[r]) l = mid+1;
else r = mid-1;
}else{
//中值和左端点相等时,移动左端点,继续判断
l++;
}
}
return -1;
}旋转链表
题目:给定一个链表,旋转链表,将链表每个结点向右移动k个位置,其中k是非负数。
示例1:

示例2:

Tips:旋转链表分三步
- 遍历一次,获取链表长度(同时获取到链表的最后结点,指向原头结点,形成环)
- 根据移动长度k计算断开链表的位置 n - k % n
- 遍历到断开链表的前置结点,赋值头结点并将前置结点指向null
public ListNode rotateRight(ListNode head, int k) {
//先获取链表长度,用移动长度k对链表长度取模,得到真实移动长度
//使用指针移动到真实长度处,将链表解开,作为新链表头部,并把原链表头部接到尾部
//记录头结点,记录尾结点
//执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
//内存消耗:37.9 MB, 在所有 Java 提交中击败了74.89%的用户
if(head == null || head.next == null) return head;
//获取链表长度,及尾结点
ListNode p = head;
ListNode end = null;
int count = 1;
while(p.next != null){
p = p.next;
count++;
}
end = p; //获取尾结点(此处也可以将链表成环)
if(k % count == 0) return head;
//找到需要解链的位置,移动一位,则解开n-1处的链,解开n-1的链,则要找到n-2处结点(前置节点)
int num = count - (k % count);
p = head;
for(int i = 0; i < num-1; i++){
p = p.next;
}
//尾结点 -> 头结点
//头结点 -> 前置节点的下一节点
//前置结点置空,作为新链的尾结点
end.next = head;
head = p.next;
p.next = null;
return head;
}旋转字符串(左旋)
字符串的左旋操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋操作的功能。比如,输入字符串
“abcdefg”和数字2,该函数将返回左旋两位得到的结果"cdefgab"。示例1:

示例2:
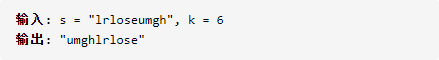
Tips: Java 中字符串是不可变的,不能像数组那样使用原地多次反转来实现旋转,字符串要使用空间
- 根据字符串长度获取实际需要移动长度,字符串相应位置即变成第一个字符
- 使用新的字符串从新字符串头部加到字符串结束,然后再从头开始添加,循环一周即可
- 可以使用取余方法将两个循环合并成一个
public String reverseLeftWords(String s, int n) {
//字符串左旋操作
//查找位置,进行两部分的遍历拼接,返回新字符串
//执行用时:5 ms, 在所有 Java 提交中击败了21.60%的用户
//内存消耗:38.3 MB, 在所有 Java 提交中击败了74.95%的用户
int index = n % s.length();
if(index == 0) return s;
StringBuffer sb = new StringBuffer();
// for(int i = index; i < s.length(); i++){
// //char c = s.charAt(i);
// sb.append(s.charAt(i));
// }
// for(int i = 0; i < index; i++){
// //char c = s.charAt(i);
// sb.append(s.charAt(i));
// }
//可以用取余操作将两个循环合并
//执行用时:7 ms, 在所有 Java 提交中击败了13.38%的用户
//内存消耗:38.1 MB, 在所有 Java 提交中击败了88.72%的用户
for(int i = index; i < s.length() + index; i++){
sb.append(s.charAt(i%s.length()));
}
return sb.toString();
}旋转字符串(旋转匹配)
题目:给定两个字符串A和B,A的旋转操作就是将A最左边的字符移动到最右边,例如,若A=
abcd,在移动一次后结果就是bcda。如果在若干次旋转操作之后,A能变成B,就说明A可以旋转成B,返回True。
Tips:这个题可以转换成字符串匹配的题目
- 遍历方法
- 遍历A字符串所有可能的旋转字符串,与B进行比较
- 在B中找到A字符串所有首字母,根据位置旋转B字符串,结果与A比较(旋转字符串思想)
- A+A这个长字符串包括所有A旋转后的结果,判断B是否在A+A中
- 可以使用
str.contains(str)判断- 高端进阶:可以使用
!!KMP!!KMP一定要学习!,算法不学KMP,…..
public boolean rotateString(String A, String B) {
//旋转字符串
//如果字符串相同,则true
//在B字符串中寻找A字符串的首字符位置
//从所有首字符位置遍历整个字符串,判断是否和A相等,相等为true
//执行用时:1 ms, 在所有 Java 提交中击败了32.14%的用户
//内存消耗:36.4 MB, 在所有 Java 提交中击败了78.81%的用户
if(A.length() != B.length()) return false;
if(A.equals(B)) return true;
char headC = A.charAt(0);
for(int i = 0; i < B.length(); i++){
char cur = B.charAt(i);
if(cur == headC && getString(B,i).equals(A)){
return true;
}
}
return false;
}
//旋转B字符串,看看是否能够旋转回到A
public String getString(String s, int startIndex){
StringBuffer sb = new StringBuffer();
for(int i = startIndex; i < s.length() + startIndex; i++){
sb.append(s.charAt(i%s.length()));
}
return sb.toString();
}旋转图像(矩阵)
题目:给定一个n X n的二维矩阵表示一个图像,将图像顺时针旋转90度。说明:你必须原地旋转图像,即需要直接修改输入的二维矩阵,不要使用另外一个矩阵来旋转图像。
示例1:

示例2:

Tips:观察发现,矩阵经过顺时针旋转90度后
- 方法一:先转置,再水平反转,就是顺时针旋转90度
- 方法二:原地旋转(!很漂亮!)
- 方法三:使用辅助数组进行旋转
- 列变成了行 即
newRow = col;- 行变成了倒数列,即
newCol = (len-1) - row
//方法一:
public void rotate(int[][] matrix) {
//旋转矩阵。
//顺时针旋转90度,相当于转置矩阵(横纵坐标互换),
//再水平反转(列反转)
//执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
//内存消耗:38.8 MB, 在所有 Java 提交中击败了41.91%的用户
//求转置,只循环上三角
for(int i = 0; i < matrix.length; i++){
for(int j = i; j < matrix[0].length; j++){
//转置是有对称轴的,即两个点元素互换
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
//水平反转,列循环一半
for(int i = 0; i < matrix.length; i++){
for(int j = 0; j < matrix[0].length/2; j++){
//转置是有对称轴的,即两个点元素互换
int temp = matrix[i][j];
matrix[i][j] = matrix[i][matrix[0].length-1-j];
matrix[i][matrix[0].length-1-j] = temp;
}
}
}
//方法二:一个循环中,四个值进行交换
public void rotate(int[][] matrix) {
//数组旋转,
//根据规律可以看出:
//(i,j) -> (j,n-1-i)
//(j,n-1-i) -> (n-1-i,n-1-j)
//(n-1-i,n-1-j) -> (n-1-j,i)
//(n-1-j,i) -> (i,j)
//即,这四个点进行了循环交换,
//找出当前矩阵中供有多少次交换
//n^2 / 4 (n是偶数时) n/2 * n/2;
// (n^2-1) / 4(n是奇数时) n/2 * (n+1)/2
//双层循环,行是n/2,列是(n+1)/2
//执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
//内存消耗:38.5 MB, 在所有 Java 提交中击败了82.59%的用户
int n = matrix.length;
for(int i = 0; i < n/2; i++){
for(int j = 0; j < (n+1)/2; j++){
//逆向替换
int temp = matrix[i][j];
matrix[i][j] = matrix[n-1-j][i];
matrix[n-1-j][i] = matrix[n-1-i][n-1-j];
matrix[n-1-i][n-1-j] = matrix[j][n-1-i];
matrix[j][n-1-i] = temp;
}
}
}


