经典排序算法

快速排序、堆排序、归并排序

排序算法

排序数组

给你一个整数数组nums，请你将该数组升序排列。

力扣912：排序数组

示例1：

示例2：

Tips：常见的排序算法都可以，但是尽量使用性能更好的快排、堆排序、归并排序。

快速排序（重要）

思想：递归思想，

• 递归结束条件：左端点大于等于右端点，说明只有一个元素，结束
• 对0至n-1的元素进行排序，选择第一个数作为基准值pivot
• 使用左右双指针，只要满足左边位置小于右边，就进行循环
  • 右指针从右端点向左检查，发现小于基准值的就覆盖到左边，右指针停止占位
  • 左指针从左端点向右检查，发现大于基准值的覆盖掉右指针处值，左指针停止占位
  • 循环结束后左右指针重合，将基准值放入此处，完成一轮循环
• 以上一轮基准元素确定的位置为中心，左边排序，右边排序

public int[] sortArray(int[] nums) {
    //手写快排，类库中sort方法也是封装的快排
    //以第一个为基准，右侧元素进行排序，找到当前元素的位置
    //递归至只有一个元素
    //执行用时：5 ms, 在所有 Java 提交中击败了92.45%的用户
    //内存消耗：46 MB, 在所有 Java 提交中击败了60.89%的用户
    quickSort(nums,0,nums.length-1);
    return nums;
}

public void quickSort(int[] nums, int l, int r){
    //只剩一个元素需要排序时，递归终止
    if(l >= r) return;

    //使用左端点值作为基准值
    int pivot = nums[l], start = l, end = r;
    while(start < end)&#123;
        //从右边找到小于基准的数值
        while(start < end && nums[end] >= pivot) end--;
        nums[start] = nums[end];
        //从左边找到大于基准的数值
        while(start < end && nums[start] <= pivot) start++;
        nums[end] = nums[start];
    &#125;
    //基准值放入确定位置
    nums[start] = pivot;

    //左边快排
    quickSort(nums,l,start-1);
    //右边快排
    quickSort(nums,start+1,r);
&#125;

堆排序（重要）

思想：堆是存储在数组中的，但是结构是树的思想。

• 大（小）根堆则有：根节点比左右子节点都大（小），子节点也满足。

• 根堆在数组中，i位置点的左子节点是2*i+1，右子结点是2*i+2

使用堆进行排序时：可建大根堆或小根堆，具体步骤：

• 对整个数组建立根堆，
  • 根据堆的二叉树思想从n/2位置处，向前遍历，因后边一半都是叶子结点
  • 判断：如果当前节点左子节点i*2+1小于堆长度，说明存在；右子节点同理
  • 遍历过程中判断当前结点和其左右子节点值大小，将最大的放在根上（即当前位置）
  • 如果与子节点进行了交换，则要跟踪交换后的位置，为根时是否满足大根堆的条件（连续下沉）
• 建堆完成后，将根（最大值）与最后一个结点进行交换（最大值就应该放在最后）
  • 数组长度-1，然后进行根堆的重建（结点的下沉）
  • 以以一个结点为根，长度为len-1，进行大根堆的建立（调整堆）（与建堆时方法一致，复用）
  • 最后循环至数组长度为len=1，完成排序
• 主要核心内容：
  1. 建堆，即从第一个非叶子节点开始进行调整堆（连续下沉）
  2. 将最大值（根）换到最后一位，堆长度-1
  3. 对整个堆进行调整（连续下沉）
  4. 循环2、3步骤

public int[] sortArray(int[] nums) {
    //使用堆排序，建堆，动态调整堆（下沉法）
    //执行用时：10 ms, 在所有 Java 提交中击败了30.65%的用户
    //内存消耗：45.7 MB, 在所有 Java 提交中击败了80.61%的用户
    //首先，建立一个大根堆
    buildMaxHeap(nums);
    //然后，将大根堆的根（最大值）与最后一个值交换，堆长度减一
    int len = nums.length-1;
    while(len > 0){
        int temp = nums[0];
        nums[0] = nums[len];
        nums[len] = temp;
        len--;
        adjectHeap(nums,0,len);
    }
    return nums;
}

//堆排序
//建立大根堆
public void buildMaxHeap(int[] nums){
    for(int i = nums.length/2; i >= 0; i--){
        adjectHeap(nums,i,nums.length-1);
    }
}
//调整堆（根-最大值与最后一个值交换），使用下沉法调整n-1个结点
//指定形成堆/调整堆的区间，即从i-len范围内
public void adjectHeap(int[] nums,int i, int len){
    //非叶子节点时去判断是否要下沉,即当前i的左子节点是否在i-len范围内，
    //不在说明i不是非叶子节点（当前范围堆中的非叶子节点）
    while(i*2+1 <= len)&#123;
        //从第一个非叶子节点（当前i结点）开始，
        //将子节点中大于当前值 且 最大的值换上来，
        //然后判断换下去的值在其位置上是否是满足大根堆（连续下沉方法）
        //如果当前结点时最大值，没有下沉，则不需要继续判断
        //如果下沉到叶子结点了，也不需要再判断
        int max = i;
        //判断左子节点是否更大
        if(i*2+1 <= len && nums[i*2+1] > nums[max]) max = i*2+1;
        //判断右子节点是否更大   
        if(i*2+2 <= len && nums[i*2+2] > nums[max]) max = i*2+2;

        //如果需要下沉
        if(max != i)&#123;
            int temp = nums[i];
            nums[i] = nums[max];
            nums[max] = temp;

            //当前i要跟踪下沉到的新位置，判断是否需要继续下沉
            i = max; 
        &#125;else break;    //如果不需要下沉，说明以当前i为根的，已经是大根堆了
    &#125;
&#125;

归并排序（重要）

归并排序是利用了分治的塑像来对序列进行排序，将一个长为n的待排序的序列，我们将其分解成两个长度为n/2的子序列。每次递归调用函数使两个子序列有序，然后我们再线性合并两个有序的子序列使整个序列有序。

具体实现步骤：

• 针对一个长度为n的序列进行排序时，
• 取序列中值，递归使用margeSort方法来对前半部分排序，递归使用margeSort方法对后半部分排序
• 对已经排好序列的[l-mid]和[mid+1,r]，使用双指针的思想合并两个有序数组
  • 两个指针起始位置比较大小，取值小的加入临时数组，指针前进，
  • 至其中一个指针到达终点，将另外一部分值全部添加到后边
  • 将临时数组中有序值复制到原数组中，最后整个数组就是有序的

public int[] sortArray(int[] nums) {
    //使用归并排序
    //对前后两部分分别排序，有序后使用双指针思想合并两个有序数组
    //执行用时：8 ms, 在所有 Java 提交中击败了44.08%的用户
    //内存消耗：45.7 MB, 在所有 Java 提交中击败了85.15%的用户
    margeSort(nums,0,nums.length-1);
    return nums;
}

//归并排序
public void margeSort(int[] nums, int l, int r){
    if(l >= r) return;

    int mid = (l+r) / 2;
    //递归排序前半部分和后半部分
    margeSort(nums,l,mid);
    margeSort(nums,mid+1,r);

    //合并两个有序数组（双指针思想）
    int i = l, j = mid+1;
    int[] temp = new int[r-i+1];//临时数组可以定义成最长全局变量，每次使用长度不同
    int index = 0;
    //合并两个有序数组
    while(i <= mid && j <= r)&#123;
        if(nums[i] <= nums[j]) temp[index++] = nums[i++];
        else temp[index++] = nums[j++];
    &#125;
    while(i <= mid) temp[index++] = nums[i++];
    while(j <= r) temp[index++] = nums[j++];

    //将排序好的序列从临时数组移动至源数组
    for(int count = 0; count < temp.length; count++)&#123;
        nums[l+count] = temp[count];
    &#125;
&#125;

快排的应用

求解TopK问题（请看TopK问题专栏）

把数组排成最小的数

输入一个非负数整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。

力扣-剑指Offer45：把数组排成最小的数

示例1：

示例2：

Tips：可以使用快排的思想，把数组中数字作为字符串，进行字符串之间的比较，将数组中字符串排序，最终得到有序的字符串排列就是最小数

• 在比较x,y大小时，使用 x+y 和 y+x 进行比较，如 "3"+"30" = "330" 大于 "30"+"3" = "303" ,因此"3"大于"30"
• 使用快排进行字符串排序，求得结果
• 使用了Java中字符串比较方法str1.compareTo(str2);
  • 结果=0:相等
  • 结果>0:str1>str2
  • 结果<0:str1<str2

public String minNumber(int[] nums) {
        //把数组排成最小的数
        //如30，3排列要比3，30小，可以用字符串拼接303，330来比较大小
        //按照给定的顺序来将字符串数组进行排序，最后按照顺序输出即可
        //执行用时：5 ms, 在所有 Java 提交中击败了97.69%的用户
        //内存消耗：37.9 MB, 在所有 Java 提交中击败了89.79%的用户
        //将数字数组转成字符串数组
        String[] strs = new String[nums.length];
        for(int i = 0; i < nums.length; i++)&#123;
            strs[i] = Integer.toString(nums[i]);
        &#125;

        quickSort(strs,0,strs.length-1);

        //也可以使用Java自带API，排序方法Arrays.sort()，传入排序的比较器
        //执行用时：6 ms, 在所有 Java 提交中击败了85.26%的用户
        //内存消耗：38 MB, 在所有 Java 提交中击败了86.94%的用户
        //可见API还是比自己手写要慢一些的，应该时封装的比较好
        //Arrays.sort(strs,(x,y) -> (x+y).compareTo(y+x));    

        StringBuffer sb = new StringBuffer();
        for(int i = 0; i < strs.length; i++)&#123;
            sb.append(strs[i]);
        &#125;
        return sb.toString();//StringUtils.join(strs,"");
    &#125;
    //快排思想排序
    public void quickSort(String[] strs, int start, int end)&#123;
        if(start >= end) return ;
        int l = start, r = end;
        String pivot = strs[l];
        while(l < r)&#123;
            //如果右端有小于基准值的，则交换之
            while(l < r && (pivot + strs[r]).compareTo(strs[r] + pivot) <= 0) r--;
            strs[l] = strs[r];
            //如果左侧有大于基准值的，则交换之
            while(l < r && (pivot + strs[l]).compareTo(strs[l] + pivot) >= 0) l++;
            strs[r] = strs[l];
        &#125;
        strs[l] = pivot;
        quickSort(strs,start,l-1);
        quickSort(strs,l+1,end);
    &#125;

堆排序的应用

求解TopK问题（请看TopK问题专栏）

根据字符出现频率排序

给定一个字符串，请将字符串里的字符按照出现的频率降序排列。

示例1：

示例2：

示例3：

Tips：

• 对于统计频率的问题，可以使用桶排序方法，先确定最大频率后根据最大频率创建桶，按照固定顺序输出。
• 使用堆排序（优先队列），根据字符的出现频率进行排序，建大根堆，最终依次输出堆的根节点

归并排序的应用

求数组中翻转对的数量

题目：给定一个数组nums，如果i<j且nums[i] > 2 * nums[j] 我们就将 (i,j)称作一个重要翻转对。你需要返回给定数组中的重要翻转对的数量。

力扣493：翻转对 （困难）

力扣-剑指Offer51：数组中的逆序对 （思想一样）

示例1：

示例2：

Tips：翻转对要求的是 i小于j的情况下，nums[i] > 2 * nums[j]

• 针对当前i，只需要考虑i之后的数字是否满足，而当其后元素有序时更容易计算

• 因此我们结合归并排序的思想，在每次分治排序时求出每个小数组中的翻转对数量

• 每次合并之前，要计算 前一个数组和后一个数组 中元素跨区间的翻转对数量

  • 如[1,2,3]和[2,3,5]合并时，合并之后的翻转对等于两个数组各自的翻转对数
  • 再加上1,2,3分别在[2,3,5]中的翻转对数量，后边数组下标都大
  • 就是[1,2,2,3,3,5]中总的翻转对数量

• 总的算法步骤：

  • 针对整个数组进行归并排序
  • 递归针对前一半和后一半进行归并排序
  • 针对两个有序数组，累计计算跨区间的翻转对数量 （每次合并完后，之前的跨区间就变成了当前数组对应的数量）
  • 合并两个有序数组

  （这个思想想起来很困难呐~）

public int reversePairs(int[] nums) {
    //归并排序进行计算
    //执行用时：59 ms, 在所有 Java 提交中击败了63.72%的用户
    //内存消耗：48 MB, 在所有 Java 提交中击败了61.96%的用户
    return margeSort(nums,0,nums.length-1);
}

//使用归并排序进行计算
public int margeSort(int[] nums,int l, int r){
    if(l >= r) return 0;

    int mid = (l+r) / 2;
    //递归使用归并排序
    int n1 = margeSort(nums,l,mid);
    int n2 = margeSort(nums,mid+1,r);

    //累计计算翻转对
    int cur = n1 + n2;
    int  m = mid+1;
    for(int i = l; i <= mid; i++)&#123;
        //这样就没有这个精髓了，还是超时的
        // for(int j = mid+1; j <= r; j++)&#123;
        //     if((long)nums[i] > (long)nums[j] * 2)&#123;
        //         cur++;//j-(mid-1);
        //     &#125; 
        // &#125;

        //这样，才能充分使用这个有序的序列(精髓)
        while(m <= r && (long)nums[i] > (long)nums[m] * 2) m++;
        cur += m-(mid+1);
    &#125;

    //合并两个有序数组
    int i = l, j = mid+1;
    int[] temp = new int[r-l+1];
    int index = 0;
    while(i <= mid && j <= r)&#123;
        temp[index++] = nums[i] <= nums[j] ? nums[i++] : nums[j++];
    &#125;
    while(i <= mid) temp[index++] = nums[i++];
    while(j <= r) temp[index++] = nums[j++];

    //临时数组中的有序序列写入原数组中
    for(int k = 0; k < temp.length; k++)&#123;
        nums[l+k] = temp[k];
    &#125;

    return cur;
&#125;

求解TopK的算法

数组中的第K个最大元素

题目：在未排序的数组中找到第k个最大的元素。请注意，你需要找的是数组排序后的第k个最大的元素，而不是第k个不同的元素。

力扣215：数组中的第K个最大元素

示例1：

示例2：

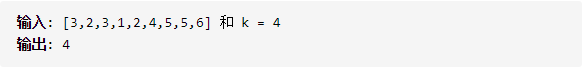
Tips：

1. 假设k总是有效的，k >= 1 && k<=数组的长度
2. 如果有相同的数，则数量累加，即 1122：最大和第二大都是2

思路：对于TopK的问题，是排序问题的变形，重点在于排序的过程，经典TopK问题可以使用快速排序或堆排序来解决

快速排序：快排的过程中，判断当前轮排序的数字位置与k的关系，

• 正好是第k个数，则返回当前数值

• 位置小于第k个数（n-k），说明第k个在右边，则对右边继续使用快排

• 位置大于第k个数（n-k），说明第k个在左边，则对左边继续使用快排

public int findKthLargest(int[] nums, int k) {
        //数组中的第K个最大元素
        //快排思想：
            //使用快排进行排序的过程中，每进行一轮排序就比较一下当前元素位置
            //如果当前元素位置是n-k，说明当前元素是第K大元素
            //如果小于 n-k，则对右边进行排序
            //如果大于 n-k，则对左边进行排序
        //执行用时：9 ms, 在所有 Java 提交中击败了36.21%的用户
        //内存消耗：38.6 MB, 在所有 Java 提交中击败了89.32%的用户
        return quickSortFind(nums,0,nums.length-1,k);
    }

    public int quickSortFind(int[] nums, int l, int r, int k){
        int pivot = nums[l], left = l, right = r;
        while(left < right)&#123;
            while(left < right && nums[right] >= pivot) right--;
            nums[left] = nums[right];
            while(left < right && nums[left] <= pivot) left++;
            nums[right] = nums[left];
        &#125;
        if(left >=0 && left < nums.length) nums[left] = pivot;
        if(left == nums.length-k) return nums[left];
        else if(left < nums.length-k) return quickSortFind(nums,left+1,r,k);
        else return quickSortFind(nums,l,left-1,k);
    &#125;

堆排序：因为是求数组中的TopK问题，堆排序更合适，可使用大根堆或者小根堆，以求第K大为例

• 大根堆：求第K大时，如果使用大根堆，则要对整个数组进行建堆（整体排序）
  • 建堆完成后，根是最大值，我们要移除最大值，然后调整堆，此时根（最大值）为实际第2大
  • 循环移除-调整堆K-1次，此时的堆根即为第K大的值
  • 建立大根堆，有点走过头又回头的意思，可以使用更方便的小根堆
• 小根堆：求第K大时，我们就以K为长度建立小根堆，此时根是前K个数中最小值
  • 查看下一个值（K+1），如果小于堆根，则不考虑，如果大于根堆，则替换堆根的值
  • 直到所有元素遍历完成，此时长度为K的小根堆，是数组中最大的K个数，堆根就是第K大的数

public int findKthLargest(int[] nums, int k) {
    //使用小根堆思想找第K大
    //执行用时：1 ms, 在所有 Java 提交中击败了99.51%的用户
    //内存消耗：38.9 MB, 在所有 Java 提交中击败了70.49%的用户
    return heapSortFind(nums,k);
}

//使用堆排序进行寻找第K大
public int heapSortFind(int[] nums, int k){
    //建立一个长度为K的堆
    buildMinHead(nums,k);
    //循环替换堆顶元素，最后调整堆为前K个最大元素
    for(int i = k; i < nums.length; i++)&#123;
        if(nums[i] > nums[0])&#123;
            //如果下一个元素大于根堆，就替换根堆的元素为较大的这个
            int temp = nums[i];
            nums[i] = nums[0];
            nums[0] = temp;
            adjectHeap(nums,0,k-1); //一直都是调整K个元素的堆
        &#125;
    &#125;
    return nums[0];
&#125;

public void buildMinHead(int[] nums, int k)&#123;
    //对前K个元素进行建堆，形成一个长度为K的小根堆
    int len = k-1; //0 -- k-1
    for(int i = k/2; i >= 0; i--)&#123;
        adjectHeap(nums,i,nums.length-1);
    &#125;
&#125; 

//从l到r，这一段序列中，判断l位置数字是否合适（调整堆，只能调整当前元素是否在确定的位置）
public void adjectHeap(int[] nums, int l, int r)&#123;
    if(l >= r) return;
    //是非叶子节点，才需要判断是否需要下沉
    while(l*2+1 <= r)&#123;
        int min = l;
        if(l*2+1 <= r && nums[l*2+1] < nums[min]) min = l*2+1;
        if(l*2+2 <= r && nums[l*2+2] < nums[min]) min = l*2+2;

        if(min != l)&#123;
            int temp = nums[min];
            nums[min] = nums[l];
            nums[l] = temp;
            l = min;    // 跟踪下沉的元素，判断是否仍然需要下沉
        &#125;else break;    //没有交换时，直接跳出循环
    &#125;
&#125;